El Dr. Aguilar Hernández es doctor en física por la UAEM. Actualmente, se desempeña como investigador posdoctoral en el Centro de Investigación en Ciencias (CInC) de la UAEM. Su área de especialidad es el análisis de sistemas complejos y series de tiempo.

El Dr. Müller es doctor en física teórica por la Universidad de Dresde, Alemania. Actualmente es profesor investigador de tiempo completo en el CInC-UAEM. Su área de especialidad se enfoca en el análisis y la simulación de sistemas complejos, con especial atención a la dinámica cerebral.

Esta publicación fue revisada por el comité editorial de la Academia de Ciencias de Morelos.

La visión antigua de la naturaleza

Hace poco, los autores conversábamos sobre algunos de los temas básicos en la licenciatura de física. Markus recordaba que en la prepa tuvo un profesor de física y matemáticas extraordinario.  Era un hombre muy estricto y exigente, pero al mismo tiempo inspirador. No solo destacaba por su precisión al enseñar, sino porque llenaba el aula con su gran entusiasmo y amor hacia las ciencias exactas y la naturaleza. La pasión y alegría con que hablaba de conceptos matemáticos y físicos eran tan contagiosos que resultaba imposible no emocionarse. Todo esto se reflejaba en la calidad de sus clases. Por ejemplo, durante su curso llegamos a ver las ecuaciones de Maxwell en su forma integral, un tema que típicamente se estudia ¡hasta el cuarto o quinto semestre de la licenciatura en física! Aquel profesor, algo corpulento, literalmente ¡bailó delante de nosotros las integrales! Gracias a su gran entusiasmo, nos quedó al menos la vaga impresión de que habíamos entendido. ¡Algo extremadamente emocionante!

Sin embargo, debemos admitir que nunca habíamos tenido clases tan aburridas como aquellas en la que se abordaron las leyes de Newton. Nos costó mucho trabajo mantenernos despiertos y evitar caer del banco. Sin duda, esto no fue culpa de nuestros profesores, más bien se debió a nuestra falta de interés y desconocimiento del tema. Y sospechamos que a muchas personas les ocurre algo similar. Paradójicamente, lo cierto es que las leyes de Newton son un tema muy fascinante. Precisamente por eso decidimos escribir en conjunto esta serie de dos artículos.

Antes de abordar el tema, quizá convenga aclarar que toda teoría científica tiene una base empírica, es decir, parte de experimentos fundamentales con resultados que no pueden deducirse teóricamente si no se establece una ley exclusivamente derivada de resultados experimentales. A partir de esa base se construye todo el edificio teórico, que a su vez permite hacer nuevas predicciones que pueden ser verificadas o refutadas experimentalmente. La deducción teórica también ayuda a explicar hechos observados en los experimentos. Algunos ejemplos de este tipo de desarrollo en la física son la electrostática, la magnetostática y la electrodinámica.

En electrostática, el experimento básico es el de Coulomb, de la cual dedujo su famosa ley enunciada en 1785. A partir de ese experimento se desarrolló toda la teoría de la electrostática, que hasta la fecha no ha sido contradicha por ningún experimento, ni siquiera en el mundo cuántico. En la magnetostática, el fundamento son las observaciones experimentales de Jean-Baptiste Biot y Félix Savart, realizadas alrededor de 1820. Y en la electrodinámica, el punto de partida fueron los experimentos realizados por Michael Faraday en 1831.

En el caso de la mecánica clásica, el fundamento son las famosas leyes de Newton. Pero, a diferencia de los ejemplos anteriores, estas leyes no se originan en un único experimento fundamental ni tampoco son resultado de la experiencia empírica directa. De hecho, al menos la primera ley de Newton es imposible de observar literalmente. Estas razones hicieron que la formulación de las leyes de Newton fuera un camino doloroso con una amplia historia que se extiende a lo largo de casi dos mil años.

La visión aristotélica de la dinámica

La historia de las leyes de Newton comienza mucho antes del nacimiento de Newton, con el erudito griego Aristóteles (384-322 a. C.), uno de los filósofos y naturalistas más influyentes de la historia. Aristóteles clasificó los movimientos terrestres en dos tipos: naturales y forzados.

En su ordenada visión del universo, cada cuerpo tenía una tendencia interna a dirigirse, mediante su movimiento natural, hacia el lugar que le correspondía: lo ligero tendía a subir y lo pesado a descender. Así explicaba que las burbujas de aire emergen en el agua mientras que las piedras caen hacia el suelo.

Aristóteles también era consciente de algunas verdades del universo, como que la Tierra es esférica, lo cual dedujo observando las sombras que la Tierra proyecta en la Luna durante los eclipses: si la Tierra fuera un disco, su sombra no sería circular sino alargada. Unos cincuenta años después, Eratóstenes (276-194 a. C.) calculó la circunferencia terrestre con un método sorprendentemente ingenioso. Estimó un valor de 39,375 km, increíblemente cercano a la estimación actual de 40,077 km.

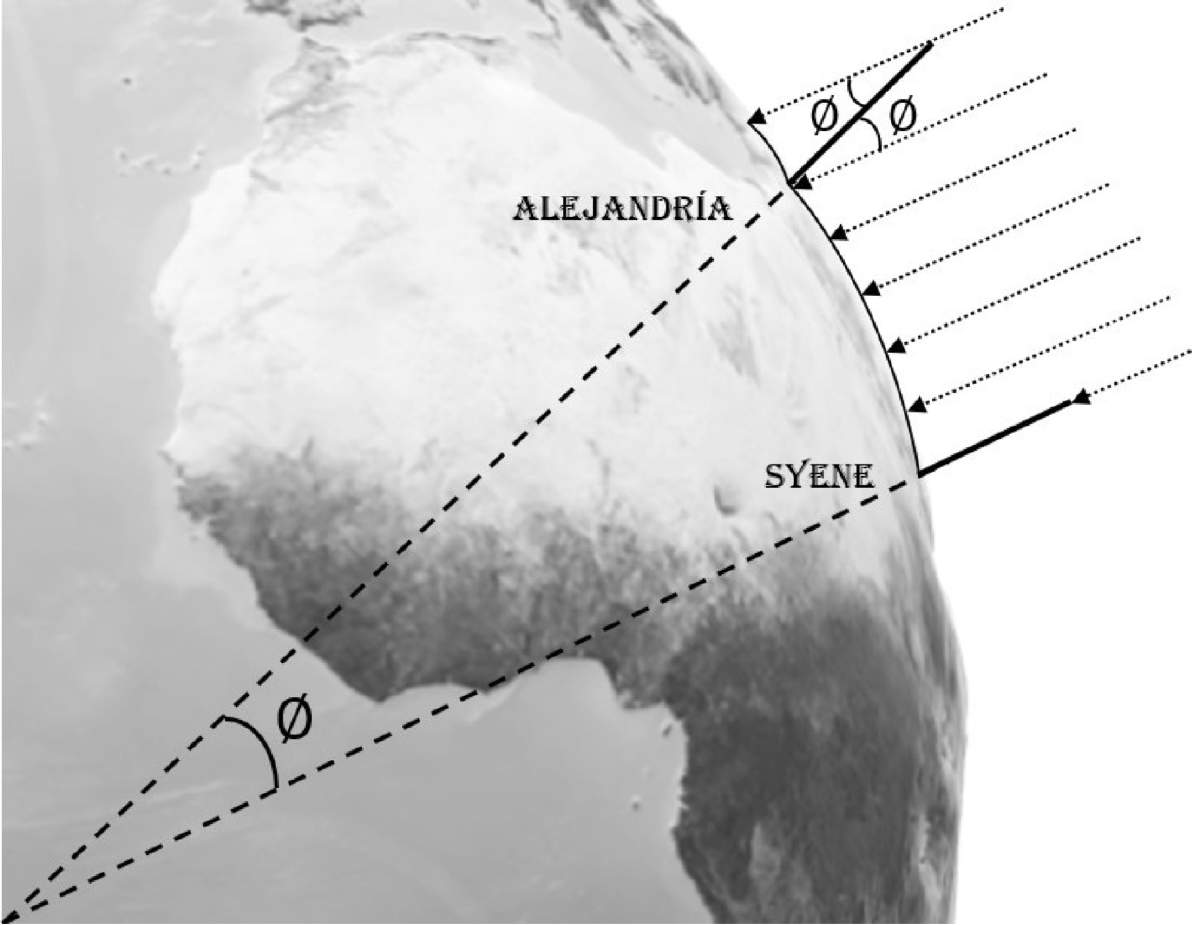
Figura 1. Ilustración del razonamiento utilizado por Eratóstenes. Elaboración propia.

Su razonamiento se basa en principios de la Geometría. Suponía que las ciudades de Alejandría y Syene (hoy Asuán) estaban ubicadas en el mismo meridiano. Esto no es completamente correcto. La ciudad de Syene se encuentra aproximadamente a 3° de la ciudad de Alejandría. Midió la distancia entre ambas ciudades alrededor de 5,000 estadios (en unidades actuales, 925 km) y colocó en cada ciudad un gnomon, un objeto vertical con una longitud de varios metros, cuya sombra se usaba como reloj solar. Al medio día del solsticio de verano observó que el gnomon ubicado en Syene no proyectaba ninguna sombra sobre el piso, lo cual significaba que el Sol se encontraba exactamente en el cenit. Sin embargo, en el mismo momento el gnomon de Alejandría sí proyectaba una sombra que podía medirse. Así pudo asignar un ángulo a la longitud de arco de 5,000 estadios, y extrapolando a un círculo completo (360°) pudo estimar la circunferencia de la Tierra (Figura 1).

Regresando a Aristóteles, él declaró que los movimientos naturales eran aquellos que se dirigían hacia el centro del universo, es decir, hacia el centro de la Tierra. Según esta visión, la Tierra estaba en un reposo absoluto ubicada en el centro del universo. Si alguien pudiera desplazar a la Tierra de su lugar, los objetos ya no caerían hacia su centro, sino al centro del universo. Si un cuerpo caía, no era por la gravedad como hoy lo entendemos, sino porque el espacio mismo tenía esa “propiedad natural”.  Curiosamente, esto nos recuerda, de manera muy lejana, las ideas de Einstein de que la gravedad modifica las propiedades del espacio… pero eso es otro tema.

Por otro lado, los movimientos forzados requerían de una fuerza externa. Un cuerpo solo podía apartarse de su posición natural, o desviarse de su movimiento natural, si algo actuaba sobre él. En este sentido, la fuerza era entendida como un esfuerzo que se tiene que realizar. Por ejemplo: si un caballo jala una carreta, ésta se mueve; si el caballo jala con más fuerza, la carreta se mueve más rápido; y si el caballo deja de jalar, entonces la carreta se detiene y queda en estado de reposo. Lo que observamos es que la velocidad parece ser directamente proporcional a la fuerza que se aplica al tirar o empujar. Si se aplica un esfuerzo constante, la velocidad se mantiene constante. Sin embargo, la velocidad alcanzada también depende de la fricción. No es lo mismo que el caballo jale la carreta por un camino llano y firme, que por un camino de arena como en la playa. Así se puede establecer que la velocidad es proporcional a la fuerza e inversamente proporcional a la resistencia del ambiente.

Es pertinente hacer dos aclaraciones: 1) En aquel tiempo no existía una definición formal de fuerza. Se asumía que la fuerza es igual al esfuerzo que una persona realiza al mover un objeto. 2) Las declaraciones se obtienen simplemente de observar la naturaleza, el caballito en este caso. Como se explica más adelante, estas afirmaciones son falsas. De hecho, el credo de la filosofía natural de Aristóteles era que no se podía aprender nada de la naturaleza mediante experimentos, ya que estos creaban situaciones artificiales y movimientos forzados que no tienen nada que ver con la naturaleza. Solo la observación pura transmitía los principios fundamentales sobre cómo funcionan las cosas.

En algunas situaciones, las ideas aristotélicas se ajustan bien a la experiencia cotidiana. Sin embargo,  presentan limitaciones evidentes. Por ejemplo, no pueden explicar por qué la velocidad de un objeto aumenta durante su caída, ni pueden explicar la dinámica del tiro parabólico. Imaginemos el lanzamiento de una piedra: primero tomamos impulso, después extendemos el brazo hacia adelante y finalmente la soltamos. Evidentemente, la piedra se mueve mientras la tenemos en la mano, lo que concuerda con las ideas de Aristóteles, ya que la causa eficiente (la persona que lanza) está en contacto directo con la piedra. Sin embargo, en cuanto la soltamos deja de haber contacto, por lo que, según Aristóteles, ya no puede ejercerse ninguna fuerza hacia adelante. Entonces, la piedra debería caer directamente hacia abajo ya que así es como por naturaleza se mueve un objeto pesado. Sin embargo, el hecho de que la piedra siga volando en una trayectoria similar a una parábola no corresponde con la teoría aristotélica. Pese a estas limitaciones, la enorme autoridad intelectual de Aristóteles hizo que sus principios dominaran el pensamiento científico durante siglos, llegando hasta la edad media, retrasando el desarrollo científico de nuevas teorías sobre el movimiento.

La teoría del “ímpetu”

A principios del siglo XIV se dio un avance importante hacia lo que hoy conocemos como la primera ley de Newton. Esto fue la llamada teoría de ímpetus, propuesta por el filósofo francés Joan Buridan (1300-1358).

El gran avance respecto a la visión de Aristóteles consistió en eliminar la necesidad de un agente externo (como la mano del lanzador) que mantuviera el contacto directo con el objeto en movimiento. La idea principal es que cuando alguien lanza una piedra, su mano le transmite un ímpetu, una especie de esfuerzo que acompaña a la piedra incluso después de haber sido soltada. Este esfuerzo o ímpetu se transmite durante el acto de poner en movimiento el cuerpo, ya sea por un primer agente (contacto directo) o por el impacto de otro cuerpo en movimiento. Pero el ímpetu no dura para siempre, se va perdiendo a lo largo de la trayectoria debido a la resistencia del ambiente (fricción), o incluso de manera autónoma (sin fricción). Es decir, un cuerpo se mueve debido a un “esfuerzo impreso” en él (ímpetu) y lo acompaña en su trayectoria hasta que se agota, posteriormente el cuerpo retorna a lo que Aristóteles llama su “movimiento natural”.

En otras palabras, si lanzamos una piedra verticalmente hacia arriba, el esfuerzo inicial, el ímpetu que le imprimimos la acompaña mientras sube. Este ímpetu se va desgastando hasta que la piedra alcanza su punto más alto (punto de retorno). A partir de ahí, comienza a descender siguiendo el movimiento natural descrito por Aristóteles. Aunque hoy sabemos que esta explicación es incorrecta según la formulación moderna de la mecánica clásica, significó un gran avance para explicar el tiro parabólico con fricción.

Buridan señaló que, debido a la resistencia del aire, la trayectoria de una piedra lanzada no sigue una parábola perfecta, sino un camino asimétrico (Figura 2). Durante la subida, tanto la velocidad vertical como la horizontal disminuyen progresivamente. Cuando la componente vertical del ímpetu llega a cero, la piedra alcanza su altura máxima y comienza a descender. A partir de este punto el movimiento de la piedra es una mezcla entre el movimiento natural y la influencia de la componente horizontal del ímpetu que aún no se desgasta. Solo cuando la componente horizontal se anula, la piedra deja de avanzar hacia adelante y la piedra sigue únicamente el movimiento natural aristotélico.

Modificado para coincidir con la medida más abajo. Originalmente aquí decía 500 estadios, lo que es incorrecto

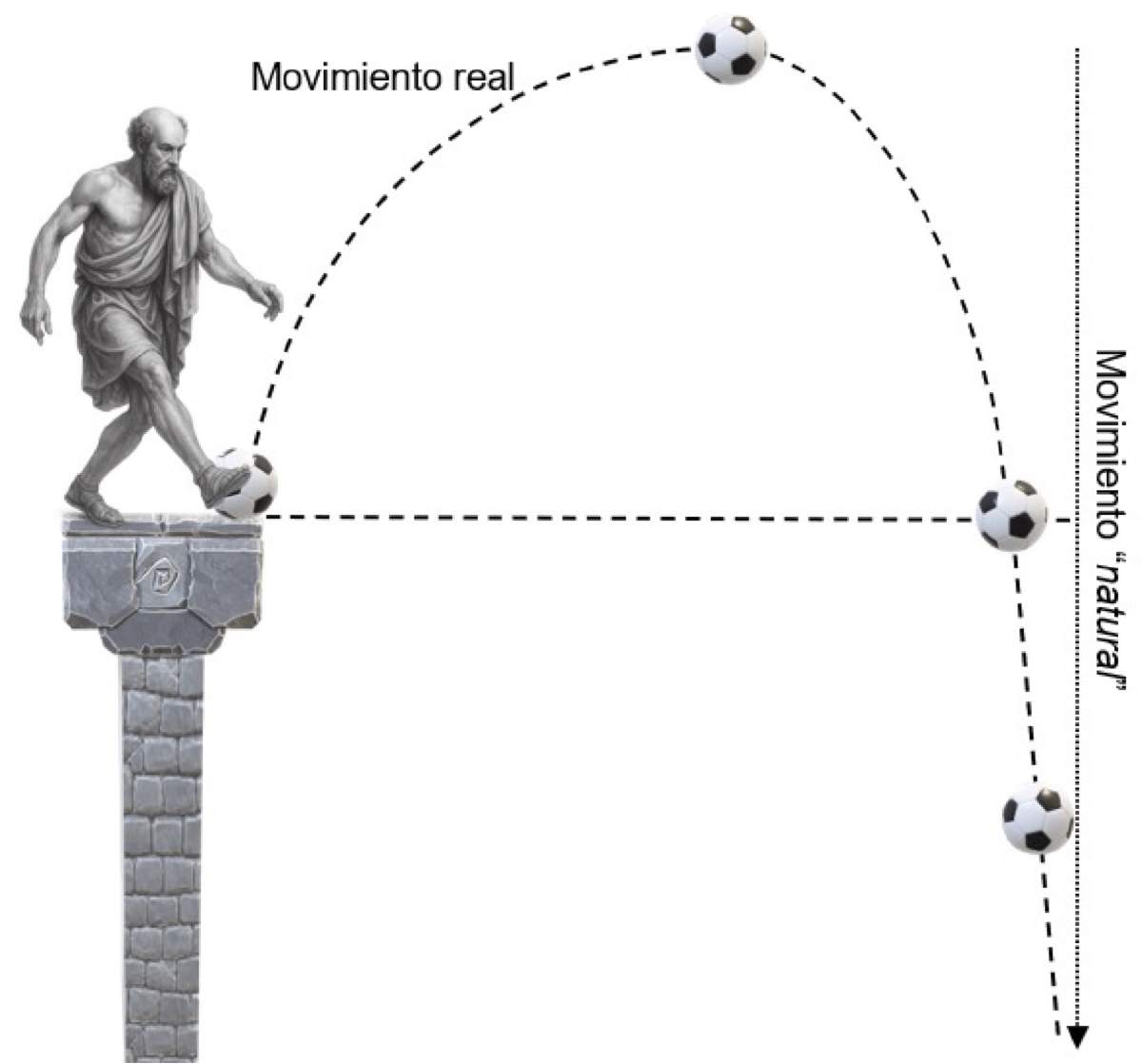
Figura 2. Comparación entre la trayectoria del movimiento real y del “natural”. Elaboración propia.

Así, la teoría del ímpetu no rompió del todo con la visión aristotélica del movimiento. Todavía conservaba la idea de que la velocidad era proporcional al esfuerzo (impreso) que se aplicaba. No obstante, representó un paso fundamental hacia una comprensión más moderna del movimiento, preparando el terreno para Galileo y, finalmente, para Newton.

Galileo Galilei, el fundador de las ciencias naturales modernas

Según Aristóteles no es posible aprender algo sobre la naturaleza a través de experimentos. Preparar un dispositivo para producir un movimiento forzado (artificial) no ofrecería información sobre los principios que gobiernan la naturaleza. Por esta razón, en tiempos de Aristóteles, realizar experimentos era visto con desconfianza, e incluso prohibido.

Quizá Galileo no fue el primero en romper con este paradigma, pero sí fue el primero en hacerlo de manera sistemática. Su razonamiento era el siguiente: si todo lo que nos rodea, incluyendo a los humanos, forma parte de la naturaleza, ¿cómo podría un experimento estar “fuera” de ella? Para Galileo, un experimento bien diseñado no oculta los principios de la naturaleza, más bien permite aislar aspectos individuales de una dinámica que, en la vida real, depende de múltiples factores. Dicho de otro modo, experimentar no es un obstáculo, sino una herramienta primordial de las ciencias naturales.

Con esta convicción, Galileo desarrolló un método sistemático para investigar los principios fundamentales de la naturaleza. Gracias a ello, no solo formuló por primera vez el principio de inercia, sino que también realizó otros descubrimientos de enorme trascendencia.

En el siguiente artículo de esta serie, seguiremos algunos de los pasos de Galileo para finalmente llegar a Newton y la formulación de sus célebres leyes. Un camino que como ya hemos visto, dista mucho de ser recto.

Para cerrar esta primera parte, hagamos un experimento ficticio, al estilo de los que tanto gustaban a Albert Einstein. Imagine que no existe ningún tipo de fricción y que frente a usted hay un bloque de cinco toneladas, un peso similar al de un elefante macho africano. Si intenta empujarlo con su dedo meñique, ¿se moverá el bloque? Regresaremos a esta pregunta la semana entrante.

Esta columna se prepara y edita semana con semana, en conjunto con investigadores morelenses convencidos del valor del conocimiento científico para el desarrollo social y económico de Morelos.