La Dra. Flores Frías es egresada de la UAEMor, donde obtuvo el título de Ingeniera Química y la Maestría y Doctorado en Ingeniería y Ciencias Aplicadas. Actualmente se encuentra haciendo su posdoctorado en el Instituto de Ciencias Físicas (ICF) de la UNAM, desarrollando síntesis de inhibidores de corrosión mediante plasma.

El Mtro. Gómez Aguilar es Ingeniero en Sistemas Computacionales (Universidad Valle del Grijalva) y Maestro en Física (Universidad Autónoma de Chiapas). Actualmente es candidato al grado de Doctor en Ciencias (Física) en el ICF-UNAM. Su investigación se enfoca en la cosmología del universo temprano, con especial atención al estudio de Agujeros Negros Primordiales y Ondas Gravitacionales.

Esta publicación fue revisada por el comité editorial de la Academia de Ciencias de Morelos.

¡Que la suerte me acompañe!

Cuando Albert Einstein dijo “¡Dios no juega a los dados!”, expresaba su incomodidad con la naturaleza inherentemente probabilística que sugería la naciente teoría cuántica. Su amigo y colega Niels Bohr, uno de los padres fundadores de esta nueva física, replicó con una frase tan célebre como provocadora: “¡No le diga a Dios qué hacer con sus dados!” Años más tarde, Stephen Hawking llevaría la frase a otro nivel al afirmar: “Dios no solo juega a los dados, sino que los arroja donde no podamos verlos” [1].

En este artículo ofrecemos un recorrido por esa frontera donde el caos se mezcla con la probabilidad, donde los algoritmos y la inteligencia artificial toman más relevancia en la solución de problemas con muchas variables.

La ilusión del control

Nadie tiene recursos infinitos.
 El profesor, en “El nuevo breviario del señor Tompkins”, George Gamow

La mente humana busca patrones. Esta tendencia, que nos permitió sobrevivir en entornos salvajes, también nos hace proclives a encontrar certezas en donde sólo hay azar. Uno de los espejos donde esto se refleja con mayor claridad es en los juegos de apuestas. ¿Qué podría ser más sencillo que tirar una moneda o apostarle a un caballo? Y, sin embargo, desde hace siglos se ha intentado construir sistemas “infalibles” para ganarle al azar.

En el libro “El nuevo breviario del señor Tompkins”, George Gamow recrea con humor y profundidad una escena doméstica donde el protagonista cree haber hallado una estrategia perfecta para apostar sin perder [2]. A continuación, se describe cómo la aparente lógica del sistema se desploma ante la realidad matemática:

“…el sistema consistía en apostar un dólar a un primer caballo. Si se ganaba, el dólar se guardaba. Si se perdía, la siguiente apuesta se duplica para cubrir la pérdida anterior y seguir asegurando una ganancia neta de un dólar. En teoría, no importaba cuántas veces se perdiera: bastaba una victoria eventual para recuperar todo lo perdido y ganar. El sistema se repetiría una y otra vez, acumulando dólares en el banco, como si el azar pudiera ser domesticado por la aritmética” [2].

Tompkins estaba convencido. Su lógica parecía impecable. Pero el profesor (su suegro), con tono sereno y experto, lo confrontó con una verdad tan simple como devastadora: ¡nadie tiene recursos infinitos! En la vida real, los jugadores se enfrentan a límites, tanto de dinero como de tiempo. Y ante una mala racha prolongada, el crecimiento exponencial de las apuestas requeridas se vuelve insostenible. Con solo 10 pérdidas consecutivas, el jugador tendría que apostar más de mil dólares; con 15, más de treinta mil. Todo, para ganar un solo dólar (Figura 1).

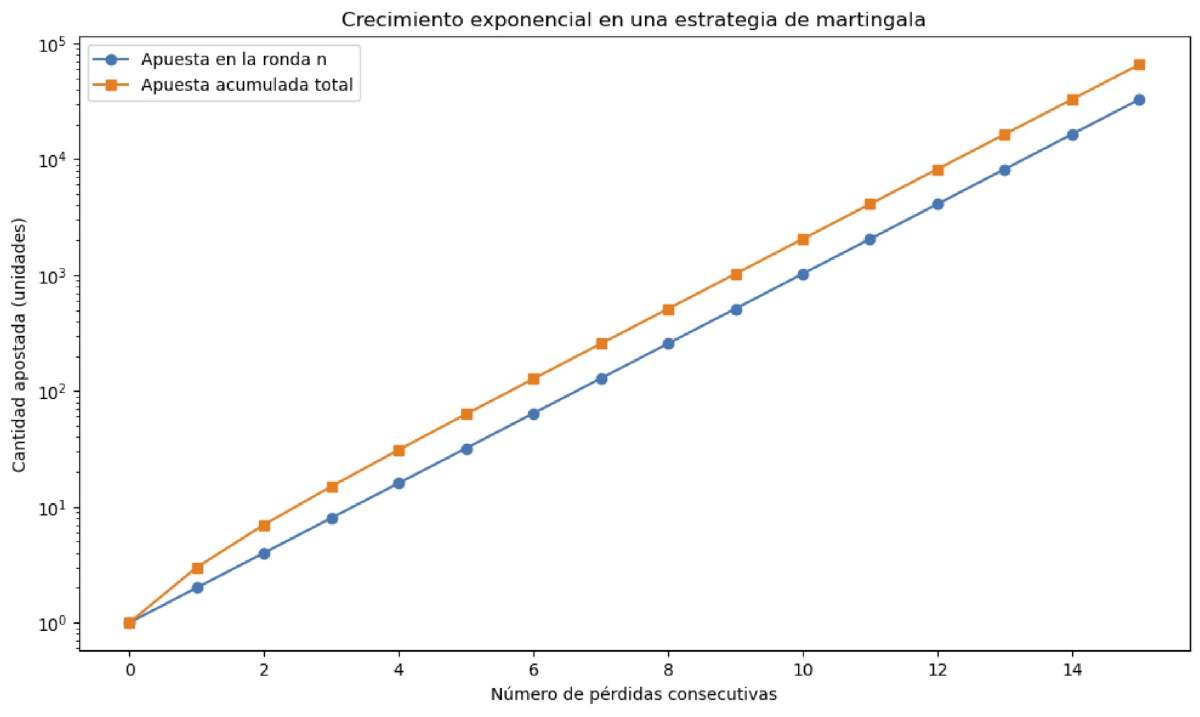
Figura 1. Crecimiento exponencial en una estrategia de martingala. La línea azul con puntos circulares muestra cuánto debe apostarse en cada ronda tras una pérdida, duplicando la cantidad cada vez. La línea naranja con cuadrados representa la suma acumulada de apuestas necesarias para alcanzar una ganancia de una unidad. Aunque el sistema parece ofrecer seguridad matemática, una simple racha de pérdidas puede llevar rápidamente a cantidades inasumibles. Esta es una manifestación de cómo un sistema simple, regido por reglas claras, puede conducir a consecuencias drásticas por su estructura interna: una antesala del caos determinista.

En teoría, siempre ganarás una sola unidad (un dólar). En la práctica, si no tienes una cantidad infinita de dinero y tiempo, tu sistema colapsará con una mala racha inevitable. Además, ningún casino permite apuestas infinitas: hay límites de mesa, número de carreras, comisiones, y lo más importante, la ley de los grandes números garantiza que eventualmente tendrás una racha de pérdidas suficiente para arruinarte.

¿Y si solo una cosa hubiese sido distinta?

Imagina que cambias de acera porque la otra está sucia. Está sucia porque alguien no pagó al barrendero; no lo pagó porque lo despidieron; lo despidieron por una cadena de pequeños hechos que empezó lejos de ti. Si tomas esa acera y no la otra, tal vez encuentres a la persona que alterará tu vida. Si un eslabón de esa cadena se mueve, ese encuentro se borra. Nada mágico: mínimos ajustes iniciales, desenlaces completamente distintos [3].

Algo parecido ocurre con la martingala del señor Tompkins. Sobre el papel todo es limpio: reglas simples, lógica impecable, promesa de “siempre ganar una unidad”. Pero el crecimiento exponencial convierte la estrategia en trampa: bastan unas cuantas pérdidas seguidas para que el capital finito, el tiempo finito y los límites de mesa la hagan colapsar. No falla la aritmética; falla nuestra intuición ante lo exponencial [2].

Ese vértigo no es exclusivo de los juegos. Muchos sistemas deterministas con reglas claras son hipersensibles a cómo empiezan: si repites exactamente el mismo estado inicial obtienes el mismo resultado, pero en la práctica nunca repites exactamente el inicio y ese ligero cambio se amplifica [4]. Edward Lorenz lo vio al redondear unos decimales en un modelo de pronóstico del clima [5]. Lo mismo pasa con un péndulo doble o con un billar de bordes curvos: un milímetro de diferencia y, en segundos, la trayectoria ya es otra [4]. En el tráfico, una microfrenada crea una ola que se propaga hacia atrás; y, al revés, una buena semaforización actúa como marcapasos temporal que impone ritmo y ordena por un rato el caos del flujo (Figura 2.) [6].

Figura 2. Marcadores de tiempo, “Cuando hacemos la parada a un autobús se introduce así una regularidad temporal, un marcapasos cuya simetría rompe el caos del tráfico…” (Idea tomada de [6]).

Bajo ese ruido también hay simetrías que sostienen el mundo sin que lo notemos: si las reglas no cambian con el tiempo, la energía se conserva; si no cambian con el lugar, se conserva la cantidad de movimiento; si no cambian con la orientación, se conserva el momento angular [6]. Por eso un trompo se mantiene estable y los planetas siguen órbitas reconocibles. Orden escondido en medio del desorden.

Algoritmos: árboles y evolución

En este sentido, vivimos en un mundo donde una sola cosa distinta redibuja el mapa. Al igual que el Sr. Tompkins, nosotros no disponemos de recursos infinitos, y en la ciencia moderna ese límite no solo es económico o energético, sino profundamente computacional: el tiempo disponible para calcular una solución antes de que el sistema evolucione, cambie o pierda relevancia. En contextos como la bolsa de valores o el mercado de derivados, donde las condiciones cambian en fracciones de segundo y los agentes interactúan en dinámicas no lineales, intentar modelar el sistema completo de manera determinista es inviable. La inteligencia artificial (IA) es el siguiente paso para llevarlo a cabo.

En la práctica, IA quiere decir usar algoritmos que aprenden patrones y exploran opciones sin revisar una por una todas las posibilidades. Su misión es podar el bosque de variables y proponer una buena respuesta antes de que cambie el juego. Dos ideas especialmente útiles por su simpleza y velocidad son los árboles de decisión y los algoritmos genéticos.

Árboles de decisión
Piensa en un sistema de cómputo que aprende solo. El sistema va tomando decisiones alternativas en base a reglas establecidas, discurriendo como entre las ramas de un árbol. El árbol descubre así qué preguntar y en qué orden para separar lo importante de lo accesorio y llegar rápido a una conclusión explicable (“si pasa A y no B, entonces C”). Para no memorizar ruido, se filtra/poda y se queda con reglas que generalizan bien. En el mercado de inversión, por ejemplo, un árbol decide “comprar / no comprar” acciones con reglas transparentes y latencia mínima [7].

Algoritmos genéticos: la evolución al servicio de la decisión
Un algoritmo genético (AG) toma una idea sencilla de la naturaleza: poblaciones de posibles soluciones que compiten, se reproducen y mutan; con el paso de las “generaciones”, la población mejora. En este algoritmo se representa cada solución como un “cromosoma” (una cadena de bits o números), definimos una aptitud que mide qué tan buena es, seleccionamos a las mejores, cruzamos sus “genes” y aplicamos una mutación aleatoria y pequeña, y posterior a ello se repite. Recomendamos a nuestros lectores revisar un artículo previo en esta sección, donde se explica con claridad y detalle más acerca de ellos [8].

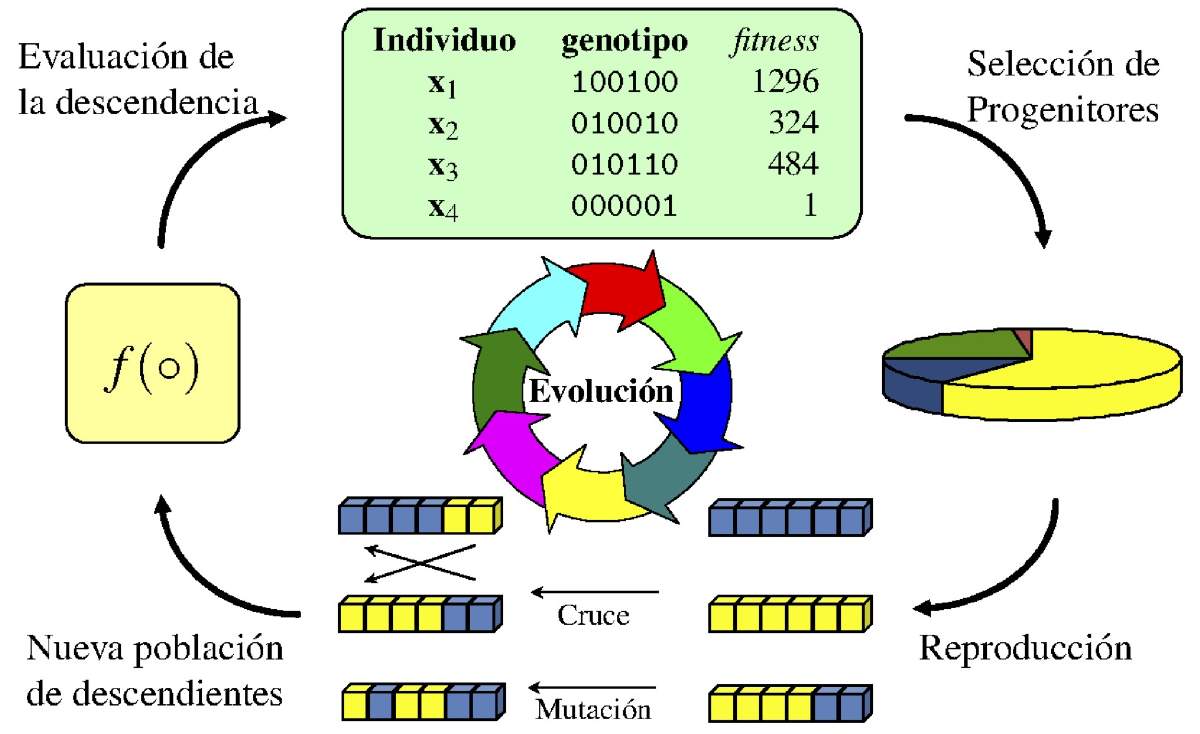
Figura 3. Esquema del funcionamiento de un algoritmo genético (AG). Cada individuo se representa mediante un genotipo (cadena de bits) y se evalúa según una función de aptitud (fitness). Los más aptos se seleccionan como progenitores, se combinan por cruce, y algunos “genes” sufren mutaciones aleatorias. Con ello se forma una nueva población de descendientes, que vuelve a evaluarse. Este ciclo iterativo de selección, reproducción, cruce y mutación permite que la población “evolucione” hacia soluciones cada vez mejores (Imagen tomada de la ref. [9]).

Frente a esa realidad, pretender controlar cada variable es imposible: el mundo es demasiado caótico y sensible a las condiciones iniciales. Por eso los algoritmos de aprendizaje automatizado, como los genéticos, funcionan como atajos evolutivos: no buscan la predicción perfecta (que nunca llega a tiempo), sino una respuesta suficientemente buena, suficientemente rápida. Igual que en la naturaleza, donde la evolución no garantiza la perfección, pero sí la adaptación, aquí lo esencial no es predecir cada bifurcación, sino sobrevivir y decidir antes de que el sistema cambie de rumbo.

Quien predice, decide

Decidir en sistemas complejos es, ante todo, jugar contra el reloj. No buscamos adivinar el futuro, sino organizar señales dispersas para elegir con sentido antes de que el escenario cambie. Ahí la inteligencia artificial resulta útil porque ordena: recoge datos históricos incompletos, capta regularidades débiles y prioriza opciones.

En sistemas como la bolsa de valores, existen muchas variables involucradas (geopolítica, confianza del consumidor, algoritmos de alta frecuencia, decisiones humanas y rumores en redes). Todo ello genera un inmenso espacio de estados, en rápida evolución. Frente a este panorama, la inteligencia artificial se ha convertido en una herramienta clave para anticipar patrones, reducir la incertidumbre y proponer decisiones automatizadas que maximicen beneficios o reduzcan riesgos. Los algoritmos de aprendizaje supervisado, redes neuronales profundas y modelos generativos intentan reconstruir las dinámicas del mercado a partir de historiales incompletos y señales indirectas. Por poner un ejemplo en México, Banxico ya incorpora la gestión de riesgos derivados del uso de IA en su marco institucional, monitoreando desde 2024 cómo esta tecnología incide en la estabilidad del sistema financiero, y subrayando que, si bien ofrece ventajas, también amplifica riesgos tradicionales como gobernanza, ciberseguridad y uso responsable de datos [10].

Esta misma lógica se replica en otros entornos complejos, como los algoritmos de recomendación en redes sociales, donde se intenta predecir el comportamiento humano (qué leerás, qué verás, qué comprarás) a partir de tus acciones previas y las de millones de usuarios similares. Sin embargo, a diferencia del entorno financiero, aquí el objetivo ya no es sólo predecir, sino influir activamente en la conducta del usuario para maximizar la permanencia, la interacción o el consumo. Se construyen perfiles psicológicos mediante análisis probabilísticos, se agrupan individuos por rasgos latentes y se optimiza cada micro-decisión del sistema en función de métricas comerciales [11]. Este enfoque, aunque computacionalmente brillante, plantea serias preguntas éticas: ¿hasta qué punto el sistema está reduciendo la incertidumbre, y hasta qué punto la está dirigiendo artificialmente para producir un resultado deseado? En última instancia, tanto en las finanzas como en las redes sociales, el problema no es la complejidad de los datos, sino el uso que se hace del poder para anticipar la toma de decisiones. En un mundo donde el tiempo y la atención son finitos, los algoritmos son jueces silenciosos que deciden qué posibilidades explorar y cuáles descartar, no siempre en nuestro beneficio.

Hoy, herramientas como la inteligencia artificial nos permiten explorar árboles de decisión imposibles para la mente humana, reconociendo patrones donde antes solo veíamos ruido. Pero ese poder no está exento de riesgos, ni de dilemas éticos. En el siguiente artículo nos adentraremos en ese territorio: cómo aprenden los algoritmos, cómo toman decisiones, y de qué manera están moldeando a la sociedad. Porque en esta nueva frontera entre lo humano y lo artificial, quizá la frase ya no sea “¿Dios juega a los dados?” sino si las máquinas están aprendiendo a lanzarlos por nosotros.

Referencias

1. Hawking, S., & Mlodinow, L. (2010). El gran diseño (1ª ed.). Editorial Crítica.
2. Gamow, G. (1976). El nuevo breviario del señor Tompkins (J. Tamayo, Trad.). Alianza Editorial. (Obra original publicada en 1965).
3. Li Zhao, A. L. El desorden ordenado: La teoría del caos. La Unión de Morelos, 5 de marzo de 2012. https://acmor.org/articulos-anteriores/el-desorden-ordenado-la-teor-a-del-caos
4. Strogatz, S. H. (2015). Nonlinear dynamics and chaos: With applications to physics, biology, chemistry, and engineering (2nd ed.). Westview Press.
5. Lorenz, E. N. (1963). Deterministic nonperiodic flow. Journal of the Atmospheric Sciences, 20(2), 130–141. https://doi.org/10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2
6. Wolf, K. B. Las simetrías ocultas y el caos. La Unión de Morelos, 3 de diciembre de 2007. https://acmor.org/articulos-anteriores/las-simetr-as-ocultas-y-el-caos
7. Wikipedia contributors. (2024, 11 de agosto). Árbol de decisión. En Wikipedia, la enciclopedia libre. https://es.wikipedia.org/wiki/Árbol_de_decisión
8. Garduño Juárez, R. Algoritmos genéticos. La Unión de Morelos, 3 de septiembre de 2012. https://acmor.org/articulos-anteriores/algoritmos-gen-ticos
9. Sancho Caparrini, F. (s. f.). Algoritmos genéticos. MatematIA (Universidad de Sevilla). https://www.cs.us.es/~fsancho/Blog/posts/Algoritmos_Geneticos.md.html
10. Juárez, E.  Banxico ya incorpora en su gestión de riesgos los derivados del uso de la IA. El Economista, 12 de junio de 2025. https://www.eleconomista.com.mx/sectorfinanciero/banxico-incorpora-gestion-riesgos-derivados-ia-20250612-763542.html
11. Veale, M., & Borgesius, F. Z. (2025). How recommender systems shape attention and polarize opinion. Nature Machine Intelligence, 7, 528–536. https://doi.org/10.1038/s44271-025-00188-8

Esta columna se prepara y edita semana con semana, en conjunto con investigadores morelenses convencidos del valor del conocimiento científico para el desarrollo social y económico de Morelos.