El Dr. Aguilar Hernández es doctor en física por la UAEM. Actualmente, se desempeña como investigador posdoctoral en el Centro de Investigación en Ciencias (CInC) de la UAEM. Su área de especialidad es el análisis de sistemas complejos y series de tiempo.

El Dr. Müller es doctor en física teórica por la Universidad de Dresde, Alemania. Actualmente es profesor investigador de tiempo completo en el CInC-UAEM. Su área de especialidad se enfoca en el análisis y la simulación de sistemas complejos, con especial atención a la dinámica cerebral.

Esta publicación fue revisada por el comité editorial de la Academia de Ciencias de Morelos.

Las teorías de Aristóteles dominaron el pensamiento científico durante casi dos mil años sin tener cambios importantes. Solo unos pocos se atrevieron a cuestionarlas, pero sin lograr imponerse frente a la autoridad de Aristóteles. Incluso hubo quienes pagaron por intentarlo con su vida, como el físico matemático italiano Giordano Bruno (1548-1600).

En el artículo de la semana pasada (1), comentamos la visión antigua de Aristóteles sobre los principios básicos de las ciencias naturales. En este ensayo avanzaremos hacia la perspectiva moderna de la mecánica clásica.

El camino hacia la base de la mecánica clásica

Como señalamos en la primera parte, toda teoría científica se apoya en principios fundamentales que surgen de experimentos u observaciones fundamentales. Estos resultados empíricos se traducen a lenguaje matemático, formulando así una ley fundamental. A partir de estos principios se construye todo un edificio teórico. En el caso de la mecánica clásica, ese fundamento son las leyes de Newton.

Iniciamos con la primera ley de Newton (ley de inercia): “Todo cuerpo persevera en su estado de reposo o de movimiento rectilíneo uniforme, a no ser que sea obligado a cambiar su estado por fuerzas impresas sobre él”. Una redacción más moderna sería: “Existen sistemas de coordenadas en las que todo cuerpo sobre el que no actúa ninguna fuerza neta se mueve en forma rectilínea y uniforme o permanece en reposo. Estos sistemas de coordenadas se denominan sistemas inerciales”. Esta afirmación es bastante extraña por dos razones: 1) en su contexto histórico no estaba claro qué era una fuerza, pues el concepto aún no estaba definido con precisión; 2) dado que en la naturaleza siempre hay fricción, el fenómeno simplemente no se puede observar en un experimento real.

Esto nos lleva a preguntarnos: ¿de dónde surge la ley de la inercia? ¿cómo se llegó a esta declaración? Para acercarnos, vamos a revisar los resultados de un par de experimentos que realizó Galileo. Incluso él tuvo que actuar con cautela, ya que la visión aristotélica de la naturaleza estaba ligada a la doctrina eclesiástica. Por ello, varias de sus ideas se publicaron principalmente en forma de diálogos. Galileo expresa su postura a través de un personaje ficticio llamado Salvati. También crea otro personaje llamado Simplicio, un seguidor y defensor de la doctrina aristotélica.

A continuación, una traducción de un fragmento adaptado del diálogo entre Salvati y Simplicio, que revela la idea central del principio de inercia:

Salvati: Entonces, dígame: si tiene una superficie plana, completamente lisa, similar a un espejo, de un material duro como el acero, que no está en forma horizontal, sino ligeramente inclinada, y coloca sobre ella una bola perfectamente esférica de un material pesado y muy duro, como el bronce, ¿qué cree usted que pasaría si la dejamos libre?

Simplicio: Estoy completamente seguro de que la bola se movería por sí sola hacia el lado descendiente de la superficie plana…

Salvati: Correcto. ¿Durante cuánto tiempo y a qué velocidad continuaría moviéndose la bola? Tenga en cuenta que hablamos de una bola rodante y perfectamente lisa, así que hemos excluido todos los obstáculos externos. Del mismo modo, deseo que ignore la presencia del aire, que presenta un obstáculo en la medida en que opone resistencia a ser cortado. También ignore cualquier otro impedimento fortuito, si es que lo hubiera.

Simplicio: Continuaría moviéndose infinitamente mientras se mantenga la inclinación del plano. Y lo haría con un movimiento cada vez más acelerado.

Salvati: Entonces, si se quisiera que la bola se moviera hacia arriba en el mismo plano, ¿cree que lo haría?

Simplicio: Por supuesto que no, pero lo haría si se le empujara o jalara con alguna fuerza.

Salvati: ¿Y si se le empujara hacia arriba con un impulso violento? ¿cómo sería su movimiento y cuánto duraría?

Simplicio: El movimiento se iría debilitando y ralentizando cada vez más, porque es contrario a su movimiento natural. Además, duraría más o menos tiempo según la fuerza del impulso y el grado de inclinación del plano.

Salvati: Ahora dígame qué le sucedería al mismo cuerpo, que ha sido puesto en movimiento por un empujón, si se moviera sobre una superficie que no es inclinada ni declinada.

Simplicio: No encuentro ninguna razón para que el cuerpo se acelere o desacelere, ya que no hay ascenso ni descenso.

Salvati: Bien, pero si no hay motivo para una desaceleración, menos puede haber para un paro total del movimiento. ¿Cuánto tiempo debería seguir moviéndose el cuerpo?

Simplicio: Tanto como dure la extensión de la superficie que no es inclinada ni declinada.

¡Esa es la idea principal de la ley de inercia! Si no existe algo que provoque un cambio en la velocidad de un objeto (no hay aceleración ni desaceleración), entonces la velocidad del objeto debe permanecer constante. Volviendo al experimento mental del plano horizontal: Como no existe fricción, entonces no existe algo que pueda desacelerar al cuerpo. Por lo tanto, el cuerpo deberá moverse hasta el infinito con una velocidad constante.

Los experimentos muestran que la esencia de la inercia es: si no actúa ninguna fuerza sobre un objeto, su velocidad no cambia ni en magnitud ni en dirección. Es decir, el objeto queda en reposo o sigue una trayectoria recta con velocidad constante. Las fuerzas son la causa de los cambios de velocidad. Sólo para recordar, todavía no se ha definido con precisión qué es una fuerza, el término se usa de manera coloquial.

Para completar la segunda formulación de la ley de inercia aún falta un ingrediente. Como ya mencionamos, Aristóteles creía que el universo tenía un centro, ubicado en el centro de la Tierra. Este punto representaba para él un espacio absoluto, creado por los mismos dioses, perfecto e inamovible. En este espacio es donde se podía definir un sistema de coordenadas adecuado para observar y describir la naturaleza. Galileo, en cambio, rompió con esta idea y propuso que no existe un único sistema privilegiado. En su lugar, introdujo un número infinito de sistemas de referencia igualmente válidos: los sistemas inerciales. Un sistema inercial es aquel que está en reposo total, o que se mueve con velocidad constante con respecto al espacio absoluto.

Ambas redacciones de la ley de inercia afirman que las fuerzas son el origen de la dinámica, pues provocan los cambios de velocidad. Sin embargo, ninguna define realmente qué es una fuerza. La experiencia cotidiana nos dice que, si se aplica la misma fuerza a diferentes cuerpos, se obtienen distintas aceleraciones. Es decir, el cambio de velocidad es distinto para diferentes cuerpos.

Todo esto conduce a asignar a cada cuerpo un atributo llamado masa inercial. Cuanto mayor es dicha masa, mayor es el esfuerzo necesario para acelerar dicho objeto. Pero esto es solo una definición cualitativa, ¡aún no sabemos qué es en realidad esa masa!

Entonces, la inercia es la resistencia de un cuerpo con cierta masa inercial al cambio de su velocidad. Es decir, entre más grande sea el cambio de velocidad y más grande la masa inercial, mayor será la inercia del cuerpo. Por lo tanto, tiene sentido definir una nueva cantidad llamada impulso que sea el producto entre la masa inercial y la velocidad del cuerpo. Con esto ya llegamos a la segunda ley de Newton: “El cambio del impulso por unidad de tiempo es proporcional a la fuerza que actúa sobre el cuerpo y sucede en la dirección de dicha fuerza”.

Debemos notar que, aunque el concepto de velocidad está bien definido como el cambio de posición por unidad de tiempo, seguimos sin entender qué es la masa inercial, por lo que tampoco queda claro qué es el impulso y, en consecuencia, qué es una fuerza. ¡Es como si alguien nos explicara una palabra china usando otra palabra china!

Si supiéramos qué es la masa inercial, también sabríamos qué es una fuerza. El escape a este dilema es la tercera ley de Newton: “acción = reacción”. En otras palabras, si un agente No. 1 ejerce sobre un agente No. 2 una fuerza, entonces el agente No. 2 ejerce sobre el agente No. 1 la misma fuerza aplicada, pero en dirección opuesta.

Por ejemplo, si una niña empujara a un elefante con una cierta fuerza, entonces la niña siente la misma fuerza con la cual resiste el elefante, pero hacia ella.

¿Cómo ayuda la tercera ley de Newton a resolver el problema de aún no conocer qué es una masa inercial y qué es una fuerza? Primero, se elige un cuerpo de referencia y se define su masa inercial como la unidad (por ejemplo, un kilogramo). A partir de esta elección, todas las demás masas pueden medirse con respecto a esta unidad, utilizando un dispositivo como el que se muestra en la Figura 1.

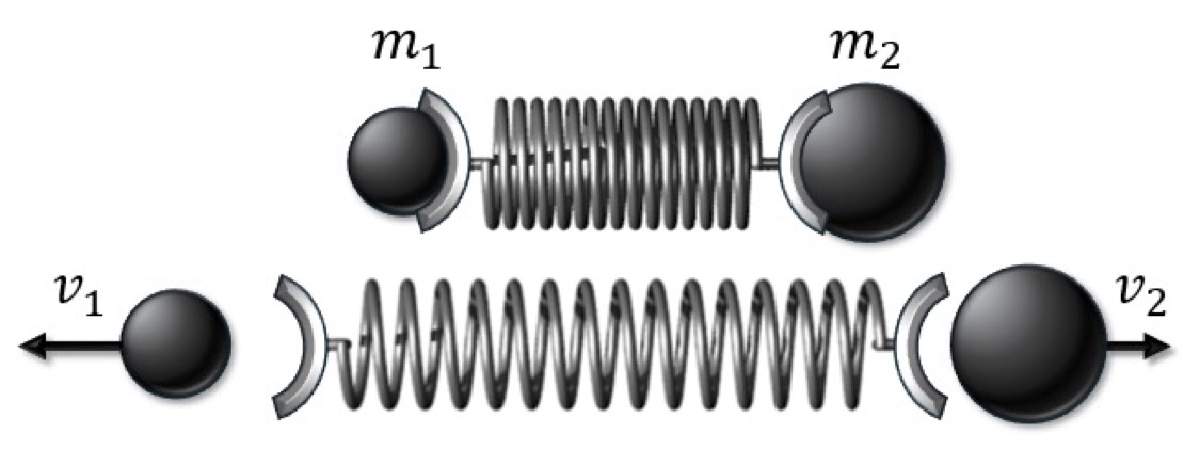
Figura 1. Esquema experimental para medir masas inerciales. Elaboración propia.

Primero se comprime el resorte colocado entre los dos cuerpos en reposo, y luego se deja expandir libremente. Después, se miden las velocidades finales de ambos cuerpos. Como ambos cuerpos partieron del reposo, el cambio de velocidad de cada uno está dado únicamente por su velocidad final. Dado que el resorte aplica la misma fuerza a cada una de las dos masas, el cambio de los dos impulsos también es igual: m₁v₁=m₂v₂.

Tomemos el cuerpo 1 como referencia, entonces podemos estimar fácilmente la masa del cuerpo 2 en unidades de la masa 1 mediante el cociente de sus velocidades. Una vez conocidas las masas, también podemos determinar las fuerzas que actuaron sobre cada cuerpo empleando la segunda ley. Con esto podemos darnos cuenta de que, si tomamos de forma individual cada ley de Newton, su mensaje es vacío porque no explican de manera autoconsistente los conceptos fundamentales. Sin embargo, en conjunto son consistentes y tienen un rico contenido filosófico y científico, presentando el fundamento de la mecánica clásica.

Haremos un último comentario con respecto al concepto de la masa. Primero, el movimiento en caída libre de una piedra no es debido al movimiento natural aristotélico, sino que está ocasionado por la fuerza gravitacional entre la Tierra y la piedra. Esta fuerza la podemos sentir al realizar el siguiente experimento: extienda el brazo derecho en forma horizontal, perpendicular a su cuerpo, y coloque un objeto en su mano (un envase de un litro de leche, por ejemplo). Probablemente no podrá mantener esta posición por mucho tiempo, rápidamente sentirá el peso del objeto, y el esfuerzo necesario para sostenerlo se hará cada vez más fatigoso (Figura 2).

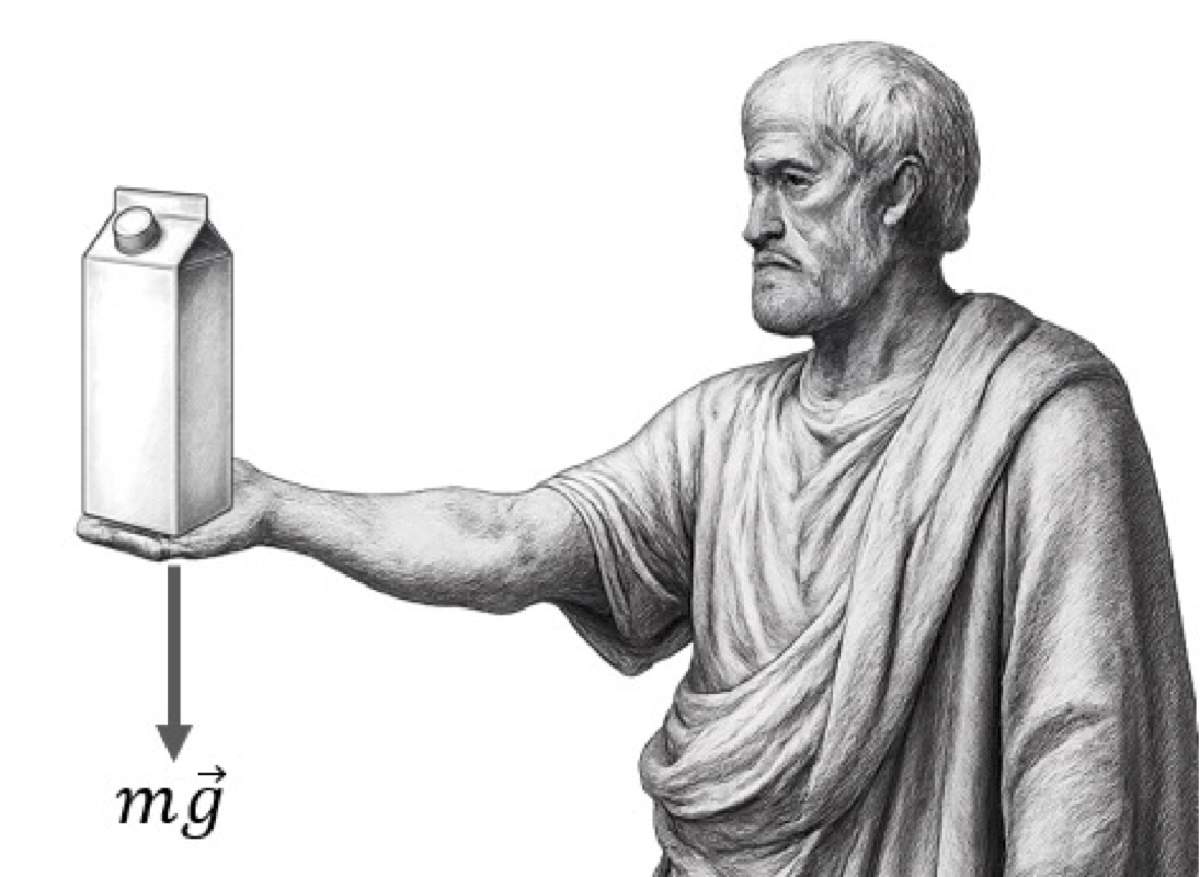
Figura 3. Ilustración del experimento referente a la masa gravitacional. Elaboración propia.

En este caso, ningún cuerpo cambia de velocidad, pues usted, su brazo y el objeto están en reposo. La fuerza total es cero porque la fuerza gravitacional se compensa con la fuerza que aplica el brazo. Pero el esfuerzo necesario para mantener esa posición depende del objeto que sostiene. Si en lugar de una botella de leche fuera un garrafón, el esfuerzo sería mucho mayor, o incluso imposible de sostener por mucho tiempo.

En resumen, aunque un objeto no esté acelerando, es necesario aplicar una fuerza para mantenerlo en su lugar (Figura 2). 

La fuerza puede calcularse mediante la ley de gravitación universal de Newton (uno de sus mayores logros), que describe la fuerza de atracción entre las masas de dos cuerpos. Esta situación no se relaciona con la inercia, pues no hay cambio de movimiento, entonces la masa gravitacional no necesariamente es igual a la masa inercial. En principio se debe hacer la distinción entre los dos conceptos, pero hacer esto no aporta mayor conocimiento sobre los principios fundamentales de la naturaleza y solo complica el desarrollo teórico. Es por esto que los físicos definieron que el valor de las dos masas sea el mismo.  Y con esto, se termina el cuento sobre las leyes de Newton.

Figura 3. Ilustración del acertijo. Elaboración propia.

Ya estamos listos para resolver el acertijo de la semana pasada, ilustrado en la Figura 3. Si no existe fricción, ¿podría la niña mover al elefante? La respuesta es un resonante sí. Si la niña aplica una pequeña fuerza, esto se traduce en la masa del elefante multiplicada por una aceleración, de acuerdo con la segunda ley de Newton. Es decir, el cociente entre la fuerza que aplica la niña y la masa del elefante es una cantidad pequeña igual a la aceleración del elefante. Pero si esa pequeña fuerza se aplica durante mucho tiempo, el elefante seguirá aumentando su velocidad, poco a poco, hasta alcanzar valores muy grandes.

De todo lo anterior podemos concluir que el camino hacia el descubrimiento de las leyes fundamentales de la mecánica clásica, las leyes de Newton, fue largo, sinuoso y lleno de obstáculos, inaccesible mediante la observación directa y repleto de conceptos filosóficos. Por eso, lejos de ser un tema aburrido, resulta fascinante.

Referencia

1. Aguilar Hernández, A. I. y M. F. Müller. Las Leyes de Newton: ¿Un tema aburrido o fascinante? Parte 1. La Unión de Morelos, 10 de noviembre de 2025. https://acmor.org/publicaciones/las-leyes-de-newton-un-tema-aburrido-o-fascinante-parte-1

Esta columna se prepara y edita semana con semana, en conjunto con investigadores morelenses convencidos del valor del conocimiento científico para el desarrollo social y económico de Morelos.